Portfolio Management
Introduction
When it comes to investing, managing one’s portfolio is the key to finding long-term stability. Portfolio management is more complex than we imagine. It is not only about managing one’s money – it involves much more such as assessing risk, measuring returns, diversifying the portfolio and other things.
This is why we have designed this module to help you understand the various nuances of portfolio management on a DIY basis.
In this module you will learn:
1. What is a portfolio?
2. What is portfolio management?
3. Objectives of portfolio management
4. Who should opt for portfolio management and why?
5. Portfolio risk and return
6. Asset allocation
7. Portfolio diversification
8. Types of portfolio management
9. Different investment styles
10. Steps to follow for portfolio management
11. Measuring portfolio performance
12. Portfolio management for risk-averse investors
13. A few helpful tips for portfolio management
So, let us understand each of the above points starting from the next unit onwards.
What Is A Portfolio?
Since we are talking about portfolios, let us begin by defining what it is. A collection of all the assets you invest in (such as shares, bonds, mutual funds, cash, fixed deposits) is called a portfolio. It is built over time and takes into account a variety of things such as:
- Investor’s risk profile
- Investment objectives
- Time horizon
- Tax treatment
- Their investment preference, such as if they are interested to invest in ESG options (Environmental, social and governance investing) or not interested to invest in certain segments such as alcohol, tobacco, etc.
What Is Portfolio Management?
Do not get confused! Portfolio and Portfolio management are entirely two different concepts. Previously we have already learned What is a Portfolio? Now, in this unit, we will study the concept of Portfolio Management. So, let us begin:
Portfolio management is the science and art of selecting and managing a group of investments to meet your short-term and long-term financial objectives. It involves making decisions with regards to your purpose of investment, balancing risk with the return, and much more.
This can be done by the investor personally or by professional portfolio managers who have vast experience in the financial markets. They use their expertise to effectively manage their clients’ portfolios to maximize return while balancing the risk exposure. To do this, they weigh the strengths and weaknesses of various investments and also take into account their opportunities and threats (SWOT Analysis). They then make an informed choice keeping in mind the client-specific constraints.
Who is a portfolio manager?
A portfolio manager is an experienced professional who understands his client’s needs, risk appetite, expected return, and other aspects and designs a suitable portfolio accordingly. He invests on behalf of his clients.
A portfolio manager earns a commission for managing a portfolio. Generally, these charges vary from 1% to 2.5% of the portfolio value but can vary from one portfolio management service to another.
Apart from investing his/her clients’ funds, a portfolio manager also counsels the client and advises them on issues such as taxation, asset allocation, accounting, financial planning, etc. The manager understands that each individual’s needs are different and there is no one size fits all approach with regards to money management.
Please note: If you opt for portfolio management, the rate of commission is something to look out for.
Objectives Of Portfolio Management
Previously we understood the concept of Portfolio Management now let us learn some of the objectives:
- To choose the right kind of assets according to a person’s age, income, budget, long-term goal, risk-taking capacity, etc.
- Aim to provide capital appreciation through earning consistent returns.
- Understanding the needs of individuals and customizing their portfolio according to the investor’s preferences and objectives.
- Balancing risk and return optimally so that an individual obtains desired returns while staying within their risk limit.
- Achieve diversification of portfolio to minimize the risk of exposure in a single asset class. This also helps clients to obtain the desired liquidity. Diversification has been discussed in detail later in this module.
- Portfolio management may also take into account tax-saving criteria, thus investing in avenues which help an individual effectively plan their taxes.
Who Should Opt. For Portfolio Management And Why?
We know you are wondering if portfolio management is meant for you. Don’t worry. You are not alone.
This is one of the most frequently asked questions by investors. You should consider portfolio management if you fall into any of the criteria mentioned below:

- Have limited time: If you live a busy life and have no time to monitor your investments regularly, then handing them over to a professional for management may be a good idea. While a portfolio does not need to be looked after daily, it has to be monitored at regular intervals, especially when the markets are choppy or some global incident is taking place. In case you have no time to allocate, it is always ideal to let a professional handle it for you.
- Limited knowledge: In case you are new to the world of finance and think that you do not have sufficient knowledge of different asset classes such as shares, mutual funds, commodities, ETFs, etc, then letting a professional do the job may be more ideal. You can benefit from their expertise.
- Want to diversify your portfolio: If you want to diversify your portfolio, portfolio management is definitely meant for you. Diversification requires knowledge of multiple markets, which may take years of experience to master.
- Participate in different asset classes: Sometimes as a retail investor, it is difficult to participate in markets that require high capital such as real estate. Moreover, having global exposure and making the best of opportunities available in other global countries may not be feasible. Opting for professional portfolio management helps retail clients to make use of such opportunities and participate in such markets.
However, please keep in mind that at the end of the day, it is your money that is being invested. Hence, even if a professional portfolio manager manages your portfolio, overseeing the entire process at regular intervals is always suggested.
Portfolio Risk
Some of the primary aspects to take care of while creating a portfolio are risk and return. Not only do risk and return of individual assets make a significant impact on a portfolio, but the correlation between all of them is also equally important. A portfolio that can maximize return by undertaking minimum risk is known as an ‘Efficient Portfolio’.
Let us understand each of them and see how it is relevant to portfolio management:
Portfolio Risk
Portfolio risk is the probability that the assets within a portfolio will not produce the desired returns or fail to meet an investor’s financial objective. Each asset within a portfolio, irrespective of what they are – shares or bonds – carry a certain amount of risk.
We know you must be thinking how can bonds be risky, aren’t they safe? The key is to remember that they have less risk, but still, they are not risk-free. To understand more about the debt market and risk, you can read our module on the Debt Market.
Risk is a very important aspect associated with portfolios.
Portfolio risk can be reduced through diversification, which has been discussed in detail in section 7 of this module.
Concept of Portfolio Beta
A portfolio beta calculates the volatility of a portfolio against the benchmark index. In other words, Beta is the sensitivity of an asset’s returns to the return on the market index. Beta is measured on a scale against a benchmark.
The beta of the market index i.e., the benchmark is 1.
A beta of more than 1 means that the security is more volatile compared to the index. Put another way, A beta of 1.5 indicates that if the index rises/falls by 1%, the stock is expected to rise/fall by 1.5%.
Similarly, a beta of less than 1 means the security is less volatile compared to the index.
Portfolio beta calculation
The beta of a portfolio is measured by measuring the volatility of each asset in a portfolio. It can be simply calculated by adding up the beta of each asset and adjusting it to the weights of each asset in the portfolio.
Steps to calculate portfolio beta
Beta can be calculated by following these four steps:
Find the value of each stock in your portfolio – Number of shares X share price
- This value will give you the weight of each asset in your portfolio – The value of individual shares/total value in the portfolio
- Multiply the weight of each asset (arrived at step 2) with the individual asset’s beta. You will arrive at the weighted beta of each asset.
- Add the individually weighted beta to arrive at the portfolio beta.
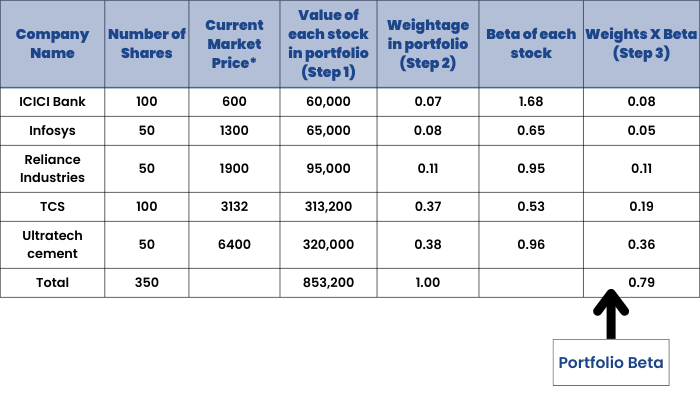
So, our portfolio’s beta is 0.79 which goes to show that it is less volatile than the market.
Portfolio Return
To put it simply, portfolio return is the gain or loss realized from the invested amount. The main objective of a portfolio is to generate returns.
How is it measured?
The expected return of a portfolio is measured by the weighted average of the expected return of individual assets (for example, shares, commodities) etc. The weights are the individual proportion of the individual assets in the portfolio, with the total portfolio weight being 100.
Portfolio return formula:
Rp = ∑ (Wi X Ri)
Where:
R = Expected return of a portfolio
P = Proportion or weights of total funds invested in security i
i = Security/Asset
Wi = Weight of security i in the portfolio
Ri = Individual return of security i
Example of portfolio return calculation:
Let us assume that there is a portfolio with a total investment of ₹ 100,000 consisting shares of 3 different companies. The details are given below:

Portfolio Return Formula = (12% X 50%) + (8% X 20%) + (10% X 30%)
Portfolio Return = 10.6%
The main purpose of calculating portfolio return is to evaluate our performance against a predetermined benchmark that is suited according to the risk undertaken by the investor. For example, if the investor’s portfolio primarily comprises blue-chip stocks, the Nifty 50 index would be an appropriate benchmark. Likewise, if the investor holds a globally diversified portfolio, the MSCI World Index would be a suitable barometer for measuring the investor’s return.
This is why you will often hear terms like “X portfolio outperformed the Sensex by 2%” which means that the returns of that portfolio in a given period is 2% more than the returns obtained by Sensex.
Portfolio Alpha
We mentioned before that return of a portfolio is usually measured against a benchmark. This measure is known as Alpha. In other words, the difference between the return of a portfolio and the benchmark is known as Alpha. A positive alpha of +4 means that the portfolio has outperformed the benchmark by 4%. A negative alpha of -4 means that the portfolio has underperformed the benchmark by 4%. An alpha of zero (0) means that the portfolio’s return is the same as the benchmark’s return.
Portfolio Alpha calculation
Alpha = R – Rf – beta (Rm-Rf)
Where:
R represents the portfolio return
Rf represents the risk-free rate of return
Beta represents the systematic risk of a portfolio
Rm represents the market return, as per a benchmark
Example of portfolio alpha calculation:
Let us continue with our previous example.
The portfolio return (R) is 10.6%
Let us assume risk-free rate of return (Rf) is 2%
The benchmark’s return (Rm) is 9%
The beta of the portfolio (Rm-Rf) is 7%
The portfolio alpha is
Alpha = R – Rf – beta (Rm-Rf) = 1.6%
Remember, the key is to obtain a higher risk-adjusted return and not total returns.
In terms of portfolio diversification, portfolio return plays a major role. The portfolio manager aims to choose assets in such a way that the performance of one is offset by the performance of another.
In our above example, if we consider asset 2 is a bond and its yield falls from 8% to 6%, the overall return of the portfolio will fall to 10.2%. Hence, instead of suffering a loss of 2%, the investor loses only 0.4%, since the drop in the return is offset by the return from asset 1 and asset 3.
Asset Allocation
Asset allocation is a very important aspect while creating and managing a portfolio. It has a direct impact on overall returns. If more money is allocated to riskier assets such as emerging market debt, small-cap stocks, cryptocurrencies, etc the return distribution of the portfolio exhibits a more prominent negative skew. In simple terms, negative skewness indicates that the portfolio will likely experience frequent small gains but infrequent large losses.
It is a well-known fact that equities outperform in a buoyant economic environment but what happens to such a portfolio when the cycle reverses, i.e., the economy goes into a recession?
This portfolio is likely to severely underperform the market as these asset classes are worst hit in a recession. It is a well-known fact that government bonds & gold perform well during periods of economic downturn. Hence, distributing funds among different asset classes such as shares, bonds, commodities, real estate, gold will help to minimize the skew and protect the investor against large losses in adverse periods.
Let us take the example of Norway’s Sovereign Wealth Fund, which is the world’s largest sovereign wealth fund with a total fund of USD 1.1 trillion. It is managed by Norges Bank of Norway. As of May 2021, the fund has invested in 9123 companies across 73 countries and 4 investment areas.
Asset allocation should take into account an investor’s risk tolerance, expected return, and time horizon.
Various methods of asset allocation:
Broadly, there are six methods of portfolio asset allocation:
1. Strategic Asset Allocation
This is the basic portfolio asset allocation method where capital is allocated proportionally into various assets based on their risk and expected return. It also takes into account the time frame. The portfolio manager can set a target and rebalance the portfolio from time to time. The portfolio manager also diversifies the portfolio and generally practices the buy and hold method to achieve the desired return.
2. Constant-Weighting Asset Allocation
This kind of asset allocation method takes into account the weights of individual assets in the portfolio. The portfolio is rebalanced based on the weights. For example, when one asset declines in value, it is purchased more to maintain its overall weight in the portfolio. There are no rules concerning timing or balancing the portfolio. However, the portfolio is reviewed from time to time to achieve the desired outcome.
3. Tactical Asset Allocation
Although portfolio managers may keep a long-term view, they may have to make tactical changes in the portfolio from time to time to take into account unusual or exceptional circumstances. This helps the portfolio managers to take advantage of sudden opportunities in the market.
This can be considered as a moderately active strategy where short-term profits can be obtained. However, this method requires significant expertise and knowledge of the market.
4. Dynamic Asset Allocation
This is also an active asset allocation strategy. In this method, the portfolio manager constantly monitors the rise and fall of the market and adjusts the portfolio accordingly. This method is heavily dependent on the portfolio manager’s judgement.
5. Insured Asset Allocation
In this asset allocation strategy, the portfolio manager establishes a base portfolio value below which the portfolio is not allowed to drop. The primary aim is to achieve a return above that base value. This method involves active portfolio management, research, forecasts, judgement, and the portfolio manager’s expertise.
So, what happens if the portfolio value drops below the base value?
The portfolio manager buys risk-free assets such as Treasury bills to bring the value up to the base value.
This kind of asset allocation methodology is suitable for risk-averse investors who don’t want their portfolio to go below a certain amount. As a result, the portfolio manager avoids risky investments, to avoid dips in the portfolio. It is important to keep in mind that by avoiding risky investments, the investor may also be foregoing potential returns that come with them.
6. Integrated Asset Allocation
This kind of asset allocation takes into account both risk in the asset mix and economic expectations. The signature aspect of this method is taking into account investor’s risk tolerance. This strategy is a combination of all the above methods and risk tolerance. Hence, it is a broader asset allocation method.
Portfolio Diversification
We discussed risk and return earlier. But how are risk and return related?
Well, risk and return are positively correlated, as in when one takes a higher risk, the return potential is also higher and vice versa. However, it doesn’t mean one has to take excessive risk to earn high returns.
Every investor should assess their risk tolerance and invest accordingly.
Portfolio diversification is the technique of reducing the risk of the overall portfolio by allocating money into different kinds of financial instruments, industries, countries, etc. The aim is to maximize returns by mitigating risk.
Diversification does not eliminate risk but instead aims to minimize it.
Let us understand this through an example. Suppose on 1st January 2020, you wanted to invest ₹1,00,000. You are new to the world of investments and always wanted to participate in the stock market. You invest half of your money in ICICI Bank Ltd. and half in ITC Ltd. On 1st January 2020, ICICI Bank closed at ₹536.75 and ITC closed at ₹ 238.15. For ease of calculation, let us assume you bought ICICI Bank at ₹535 and ITC at ₹235.
So, your investment would look something like this:
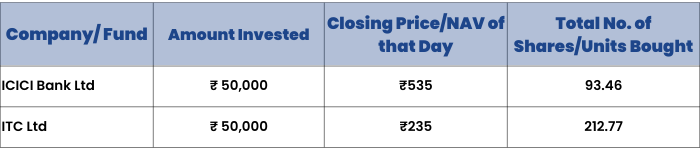
When the Covid-19 pandemic hit the world, global markets crashed, and the Indian Markets followed suit. On 23rd March 2020, the markets went down significantly. ICICI Bank closed at ₹284 while ITC closed at ₹ 154.3. So, the values of your investment in ICICI would have fallen to ₹ 26,412 and ITC would have fallen to ₹ 32,711.6.
In other words, the value of your ₹ 1,00,000 would have become ₹ 59, 123.6.

Instead, if you had split the ₹ 100,000 four ways and invested ₹ 25,000 each in ICICI Ltd shares, ITC Ltd shares, HDFC Gold ETF, and Axis Bluechip fund, what would have happened?
The closing NAV of HDFC Gold ETF on 1st January 2020 was ₹ 3521.90 and Axis Bluechip Fund was ₹35.76. For ease of calculation, let us assume you bought HDFC Gold ETF for ₹ 3,500 and Axis Bluechip Fund for ₹ 35.50.
On January 1, 2020, your investment would have looked something like this:
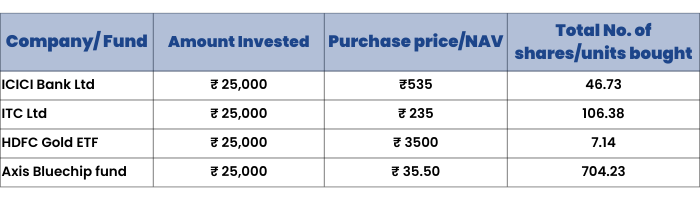
So, on 23rd March 2020, when markets fell sharply, your portfolio would have looked something like this:
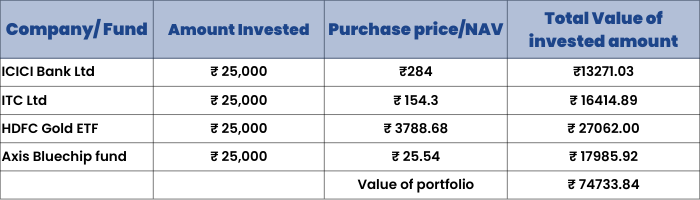
As you can see, effectively, you would have lost a much lesser amount by diversifying your portfolio.
A thing to note here is the fact that the portfolio has incurred losses in the second scenario as well, although the amount of the loss is much lesser. This brings out the fact that the purpose of diversification is to reduce risk, not eliminate it.
Purpose of portfolio diversification
As mentioned above, the primary objective of portfolio diversification is minimizing risk. When we talk about risk, we talk about two different types of risk – systematic and unsystematic risk.
Total Risk = Systematic + Unsystematic Risks
Systematic risk is the inherent risk of the entire market and reflects the impacts of several factors in the market – economic, geo-political, financial, etc. Systematic risk is generally unpredictable and is often considered as unavoidable.
Unsystematic risk, on the other hand, is a company-specific risk or the risk associated with a particular investment in a portfolio. This is the risk that can be avoided through diversification.
How many financial instruments should you include?
This is a frequently asked question with regards to portfolio management. And the answer is ‘no one knows for sure’. Naturally, having five shares is better than one. But there is no golden answer. It entirely depends on your risk appetite and your knowledge of different financial markets.
When it comes to a share portfolio, some experts opine that having 15-20 stocks is a good starting point. However, honestly speaking, this will vary from one person to another.
Types Of Portfolio Management
Portfolio management can be of various types. Here are some of the major ones:
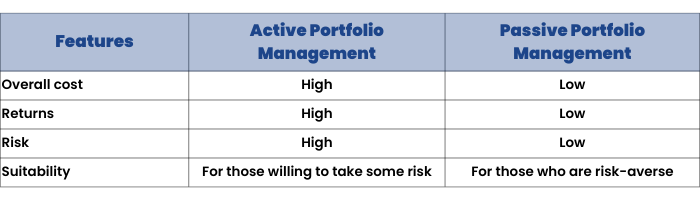
Active portfolio management
As you can understand from the name, in this kind of portfolio management, the portfolio manager actively buys and sells securities and assets to make use of opportunities in the market. Usually, the portfolio manager tracks a specific index such as the BSE Sensex or Nifty 50 and tries to outperform the benchmark index.
Since this portfolio management technique involves taking quick, yet informed decisions, usually the portfolio manager is guided by a team of co-managers as well as analysts. Extensive analysis, market forecasting, and the expertise of the portfolio management team are crucial to the success of active portfolio management. The team has to keep a keen eye on the market trends, economic changes, political landscape, corporate news, and other aspects that can affect the financial market.
Passive portfolio management
In passive portfolio management, the portfolio manager primarily designs a fixed portfolio and reviews it from time to time. In most cases, the portfolio tries to duplicate a particular market index and buys the same stocks that are listed on the index, giving them the same weightage in the portfolio as in the index.
A passively managed portfolio can look like an exchange-traded fund or ETF. Compared to actively managed portfolios, these portfolios require less oversight, a smaller team to manage and incur lower charges.
Discretionary portfolio management
In this kind of portfolio management, an individual authorizes the portfolio manager to make financial decisions on his behalf. The money is assigned to the portfolio manager. In turn, the portfolio manager takes all the investment decisions. Before commencing, a thorough analysis is done of the individual’s investment goals, time horizons, needs etc. so that an informed decision can be arrived at.
The negative aspect of discretionary portfolio management is that the portfolio manager remains in the driver’s seat, while the investor remains merely a rider. The portfolio manager controls the entire portfolio and if he is not an expert, this may be detrimental to the investment portfolio.
Non-discretionary portfolio management
In non-discretionary portfolio management, the portfolio manager acts as an advisor. He advises the client, but the client reserves the right to make the final decision.
Different Investment Styles
In the previous section, we discussed the various types of portfolio management. Apart from that, portfolio managers can adopt different styles or a combination of several of them to bring out the best results for a portfolio.
Let us now take a look at some of these styles:
Value or growth
A portfolio manager may decide to concentrate on the current value of a company (value-based investment) or its future growth potential (growth-based investment).
Size of the company- Small, Medium or Large-cap
A portfolio manager may concentrate on only large-cap stocks for a portfolio or may decide to diversify into the small and medium cap as well.
Market trends
A portfolio manager may decide to follow market trends and make investments accordingly. This is known as a momentum style. On the other hand, he/she may also decide to go against the trend, and take decisions based on his/her experience. This style is known as a contrarian style.
Momentum investing
In momentum investing, an investor buys securities that are showing an upward trend and sells them when they have peaked. The investor is always on the lookout for buying opportunities and makes use of short-term uptrends. Of course, this kind of investing style requires severe practice to spot purchasing opportunities and is quite risky.
Please note that there are many more investment styles. We have only explained a few of them above.
Steps To Follow: Portfolio Management
Whether you are managing your own portfolio or you are opting for a professional portfolio manager, here are some steps that need to be followed for efficient portfolio management.
1. Determine the investment objective
Every person is different. Be it a large portfolio or small, every investment is made with a specific objective or goal – children’s higher education, planning for retirement, family holiday, emergency fund, to name a few. Hence, the first step is to determine the investment objective. This will also help in ascertaining other aspects such as the time horizon, risk appetite, desired return, etc.
2. Choosing the asset classes
The next step involves choosing the asset classes. This depends largely on the investor’s risk appetite as well as the time horizon. As we have already seen in this module, distributing the investible fund into a variety of asset classes helps in the diversification of the portfolio.
3. Strategic asset allocation
Strategic asset allocation is the process of setting allocation into assigning a targeted allocation for each asset class in a portfolio – such as 60% into equity, 40% into bonds, and so on. Again, the percentage of allocation depends on the investor’s risk appetite, time horizon, and return expectation. Based on these weights, the portfolio is rebalanced at regular intervals.
4. Tactical asset allocation
This is a portfolio strategy wherein the weights associated with each asset class is changed to adapt to changing market conditions. For example, suppose there is a portfolio with a strategic asset allocation of 60% into equity, 20% into bond, and 20% into gold. In 2020, when global stock markets crashed due to the Covid-19 pandemic and gold showed an upward trend, the portfolio manager may have changed the allocation to 40% equity, 20% bond, and 40% gold.
This kind of change is known as tactical asset allocation. Through this kind of asset allocation, the fund manager tries to identify opportunities in the market as well as make tactical decisions to protect a portfolio from unforeseen market scenarios.
5. Measure performance
The main purpose of doing all the above steps is to generate returns. Naturally, we would want to see what we have achieved. This is the final stage where the performance of the portfolio in question is measured. A range of measures is available to determine how a portfolio is doing. This has been discussed in detail in the next section of this module.
Measuring Portfolio Performance
There are a variety of ways by which a portfolio’s performance can be measured. Over the years, different financial experts have come up with different kinds of ratios and measurement criteria to understand a portfolio’s performance. At the core of all these criteria lies the fact that investors want to achieve a maximum return by taking a minimum risk. Therefore, the methodologies which reward high return while penalizing high risk are most suitable for this purpose.
Here, we have discussed three measurement methods most widely used by portfolio managers.
Sharpe Ratio
This is probably the most commonly used measure. It was conceived by Bill Sharpe and closely follows his work Capital Asset Pricing Model.
The formula for measurement is:

Where:
PR = Portfolio return
RFR = Risk free rate of return
SD = Standard deviation
Let us understand this through an example.
Let us assume that there are 3 portfolios – A, B and C. Let us assume that the risk-free return in the market is 4%.
The individual return of each portfolio will look something like this:

Things to note:
✔A higher Sharpe Ratio represents higher returns and lower standard deviation. Hence, it is good. Thus, in the above example, Portfolio B is the best performing one.
✔Since Sharpe Ratio measures risk in terms of standard deviation, it should be used for portfolios containing many assets, not just a few.
Treynor Ratio
Treynor Ratio is also a widely used measure. It was introduced by Jack L. Treynor to provide a composite measure of portfolio performance. This measure applies to all kinds of investors, irrespective of their risk tolerance.
✔According to Treynor, there are practically only two components of risk:
- Risk produced by fluctuations in the stock market
- Risk produced by fluctuations of individual securities
The concept of a security market line was also introduced by Treynor. A security market line is drawn on a chart and shows different levels of systematic risk or market risk, plotted against the expected return of the entire market at a given time. The higher the line’s slope, the better is the risk and return trade-off.
Since the Treynor ratio takes into account the volatility factor, it is often known as the reward-to-volatility ratio.
It is measured as:

Where:
PR = Portfolio return
RFR = Risk free rate of return
β = Beta
Let us come back to our previous example, as per Treynor Ratio, the portfolio performance would look something like this:

Hence, as per Treynor Ratio, the performance of Portfolios A and B are the same.
A thing to note:
The higher the Treynor Ratio, the better is the portfolio performance.
Jensen’s Alpha
The third most commonly used measure is Jensen's Alpha. It was created by Michael C Jensen and calculated the excess return generated by a portfolio over its expected return. Truly speaking, it measures a portfolio manager’s ability to generate above-average returns, after adjustment of market risk.
Jensen’s alpha calculation:
α = PR – (RFR + β)
Where:
α = Jensen’s Alpha
PR = Portfolio return
RFR = Risk free rate of return
β = Beta

A thing to note:
✔The higher the ratio, the better is the risk-adjusted returns.
✔A portfolio that generates consistently positive excess returns will have a positive alpha. A portfolio that generates consistently negative excess returns will have a negative alpha.
Please note: All the examples provided above are the simplistic representation of the ratios. Of course, situations are much more complex in real life and hence, there can be multiple factors and variables affecting a portfolio. As the factors increase, the calculations will become more complex.
Portfolio Management For Risk-Averse Investors
Most of the things we spoke about earlier involve a certain amount of risk. But what about those investors who don’t want to take any risk?
Don’t worry, this has also been widely discussed and various theories have been formulated around these lines – the most popular being the "Modern Portfolio Theory".
Modern Portfolio Theory:
This theory talks about portfolio construction for a risk-averse investor to maximize expected return at a given level of market risk. It was pioneered by Harry Markowitz and first published in 1952. He was later awarded the Nobel Prize for this theory.
The basis of this theory is that an investment’s risk and return should not be viewed separately. Instead, it should be assessed based on the overall portfolio’s risk and return.
However, we know that risk and return are closely related when it comes to financial markets. Hence, if one opts for lower risk, he/she will obtain lower returns as well. On the other hand, riskier and more volatile investments fetch more returns. But not everyone is comfortable with such high amounts of risk.
This is where Modern Portfolio Theory suggests diversification. Hence, a portfolio may have one particular asset type which is a high risk, however, when combined with other asset types, the overall risk of the portfolio comes down. Thus, instead of holding only low-return bonds (less risky) or high-risk products such as derivatives or commodities, an investor can hold a mixture of both to earn maximum possible returns.
There are several benefits of this theory. It speaks about diversification. It also propagates reducing volatility. It works especially well if the assets in a portfolio are non-correlated. It is possible to create an efficient portfolio using this theory by choosing relatively low-risk options such as fixed deposits, Government of India bonds, etc.
However, since the formulation of theory, real-life market conditions have become much more complex. Therefore, the viability of the theory against the present-day market conditions remains a matter of doubt among portfolio managers and investors.
Guidelines For Portfolio Management
Before we conclude, let us note down a few helpful tips that will help you manage a portfolio better:
1. Understand your risk tolerance – Very important. Often we think we can take the risk, but when the market actually falls, then we cannot keep patience and make hasty decisions.
2. Be patient – Markets go up and down. That’s normal. Be patient.
3. Define your investment time horizon – A very important aspect. Make a rough timeline of when you will need the fund and invest accordingly. For example, if you need a fund for a specific purpose next year, it is better to avoid the stock market. Keeping a fixed deposit may be more suitable.
4. Choose assets you know about – Don’t go for assets because you think they are good or others are investing in them. Choose assets that you know about – how they behave, how risky they are etc. For example, these days you will see hundreds of advertisements about cryptocurrencies. You may be enticed to invest. But cryptocurrencies are highly volatile and entail a very high risk. Hence, if you don’t know about it, avoid it.
5. Learn, learn and learn – There is no end to educating oneself, especially when it comes to financial markets. Keep learning and exploring. This will help you learn about new markets and new products.
6. Keep a global perspective – There is a world of opportunities out there. Don’t restrict yourself to a specific product, asset, market or industry. A holistic viewpoint and a portfolio perspective will better help you in allocation decisions.


